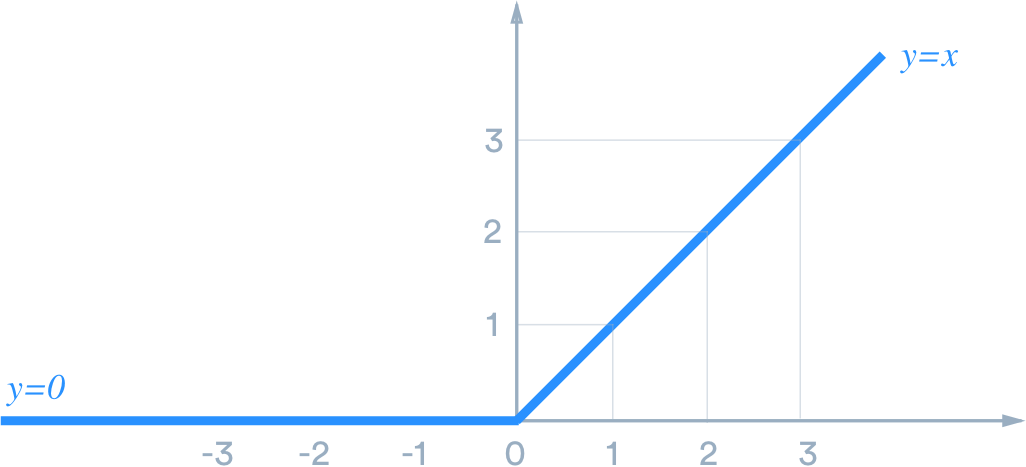
Activation Function- ReLU
This article discusses one of the most prominent activation used in Neural Networks.
Activation function
The main role of the activation function is to decide whether neural networks should be activated or not. This is inspired by biological neural networks. The choice of the different activation function is dependent on the architecture of the network and also on results one obtain using them. An activation function can be Linear and Non-Linear, but a network with linear function can only learn linear problems since summing all the layers in the network will give another linear function. whereas Non-Linearity allows the network to learn more complex problems. Some of the desirable properties of the activation function are mentioned below.
Properties of the Activation Function
-
Non-Linearity: The main purpose of the activation function is to introduce Non-linearity in the network such that the network would be capable of learning more complex patterns.
-
Continuous differentiable:Activation function should be continuously differentiable with respect to the weights for the gradient-based optimization methods.
-
Monotonic: Activation function helps the neural network to converge easier into a more precise model.
What is ReLU?
ReLU function is one of the most widely used hidden layer activation function and it is non-linear, monotonic and also continuously differentiable almost everywhere (except at 0, the left derivative at z = 0 is 0 and the right derivative is 1).
-
ReLU is called piecewise linear function or hinge function because the rectified function is linear for half of the input domain and non-linear for the other half.
-
The ReLU layer does not change the size of its input.
-
ReLU does not activate all neurons, if the input is negative it converts to zero this makes the network sparse, efficient and easy for computation.
-
ReLU is non-smoothy, can only be used in the hidden layer.
Why ReLU is popular?
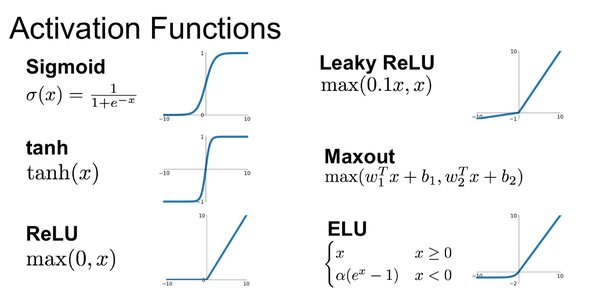
Observe the figure mentioned below to differentiate between activation functions.
-
Other activation functions like sigmoid, tanh suffer from vanishing gradient problem. Both ends of these curves are ‘almost- horizontal’. Gradient values at these parts of the curve are very small or have vanished. Because of that, the network refuses to learn further or the learning is drastically slow.
-
Rectifiers are faster, simply because they involve simpler mathematical operations. they do not require any normalization and exponential computation (such as those in sigmoid or tanh activation function).
-
The training of Neural Network on ReLU can be faster up to 6 times in comparison to other activation functions.
However, the rectifier has another problem dying ReLU problem. for argument lower than the value 0 the gradient vanishes. Neurons that went into that state stop responding to changes in input or error (i.e at gradient value 0, nothing changes).
How to solve the dying ReLU problem?
A solution for that problem is the modification in the ReLU activation function resulted in variants of the ReLU like Noisy ReLU, Leaky ReLU, ELU mentioned in fig2.
LReLU: The derivative of the LReLU is 1 in the positive part and small fraction in the negative part. Instead of being 0 when z<0, a leaky ReLU allows a small, non-zero, constant gradient α (Normally, α=0.1).
\[σLReLU (x) = max(0, x) − α max(0, −x) #Normally,α=0.1\]An advantage of using LReLU is thus that we can worry less about the initialization of your neural network. but in the ReLU case, the neural network that never learns if the neurons are not activated at the start. we may have lots of dead ReLU without even knowing.
Example: ReLU layer in a Layer array
layers = [
#28x28x1 images with 'zerocenter' normalization
imageInputLayer([28 28 1])
#20 5x5 convolutions with stride &padding
convolution2dLayer(5,20)
#ReLU Layer
reluLayer
#2x2 maxpooling with stride 2x2 and padding [0 0 0 0]
maxPooling2dLayer(2,'Stride',2)
#10 fully connected layer
fullyConnectedLayer(10)
softmaxLayer
classificationLayer
]